体育课进行篮球投篮达标测试。规定:每位同学有5次投篮机会,若
投中3次则“达标”;为节省时间,同时规定:若投篮不到5次已达标,则停止投篮;若即
便后面投篮全中,也不能达标(前3次投中0次)则也停止投篮。同学甲投篮命中率是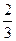 ,
,
且每次投篮互不影响。
(1)求同学甲测试达标的概率;
(2)设测试同学甲投篮次数记为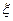 ,求
,求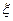 的分布列及数学期望
的分布列及数学期望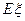 。
。
推荐套卷
体育课进行篮球投篮达标测试。规定:每位同学有5次投篮机会,若
投中3次则“达标”;为节省时间,同时规定:若投篮不到5次已达标,则停止投篮;若即
便后面投篮全中,也不能达标(前3次投中0次)则也停止投篮。同学甲投篮命中率是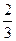 ,
,
且每次投篮互不影响。
(1)求同学甲测试达标的概率;
(2)设测试同学甲投篮次数记为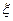 ,求
,求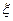 的分布列及数学期望
的分布列及数学期望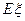 。
。