设数列{an}：1，－2，－2，3，3，3，－4，－4，－4，－4，…，(－1)k－1k，…，(－1)
，即当
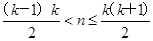(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)，用数学归纳法证明Si(2i＋1)＝－i(2i＋1)(i∈N*)．
相关试题
＝a，
＝b，求向量a与b的夹角．
.相关知识点
推荐套卷
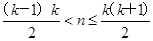设数列{an}：1，－2，－2，3，3，3，－4，－4，－4，－4，…，(－1)k－1k，…，(－1)，即当(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)，用数学归纳法证明Si(2i＋1)＝－i(2i＋1)(i∈N*)．
粤公网安备 44130202000953号