.如图1,在平面直角坐标系xOy中, 矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
 ,OA=1,OC=2,
,OA=1,OC=2, 点D在边OC上且
点D在边OC上且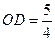 .
.
(1)求直线AC的解析式;
(2)在 y轴上
y轴上 是否存在点P,直线PD与矩形对角线AC交于点M,使得
是否存在点P,直线PD与矩形对角线AC交于点M,使得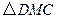 为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3) 抛物线
抛物线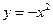 经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且
经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且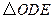 沿DE折叠后点O落在边AB上
沿DE折叠后点O落在边AB上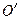 处?
处?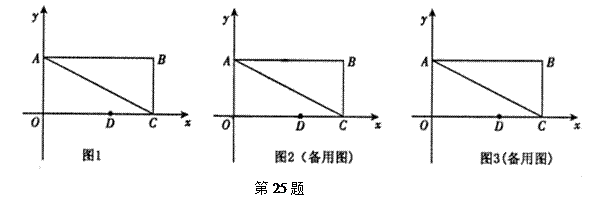
相关知识点
推荐套卷
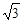 )(a+
)(a+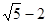 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号