2007年5月30日,在“六一国际儿童节”来临之际,某初级中学开展了向山区“希
望小学”捐赠图书活动.全校1200名学生每人都捐赠了一定数量的图书.已知各年级人数比例分布扇形统计图如图①所示.学校为了了解各年级捐赠情况,从各年级中随机抽查了部分学生,进行了捐赠情况的统计调查,绘制成如图②的频数分布直方图.根据以上信息解答下列问题: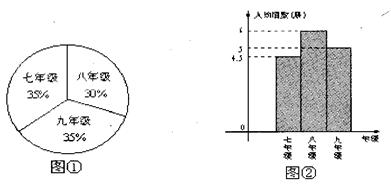
(1)从图②中,我们可以看出人均捐赠图书最多的是_______年级;
(2)估计九年级共捐赠图书多少册?
(3)全校大约共捐赠图书多少册?
相关知识点
推荐套卷
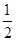 ,2,
,2,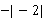 ,
,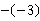 ,0在数轴上表示出来,并用“<”把它们连接起来.
,0在数轴上表示出来,并用“<”把它们连接起来.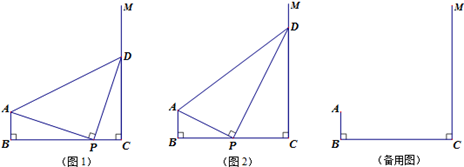
 粤公网安备 44130202000953号
粤公网安备 44130202000953号