如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.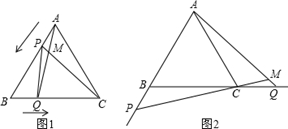
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
相关知识点
推荐套卷
 中,抛物线
中,抛物线 过点
过点 (0,4)和
(0,4)和 (8,0),P(t,0)是
(8,0),P(t,0)是 轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作
轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作 轴的垂线,两直线相交于点D.
轴的垂线,两直线相交于点D.

 为何值时,点D落在抛物线上?
为何值时,点D落在抛物线上?  .过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
.过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
 的大小;
的大小; 的延长线上取一点
的延长线上取一点 ,以
,以 为角的一边作
为角的一边作 ,另一边交BD延长线于点E, 若、
,另一边交BD延长线于点E, 若、 (如本题图②所示),试求
(如本题图②所示),试求 的值(用含
的值(用含 的代数式表示).
的代数式表示). 中,
中, ,
, .
.
 为直径的⊙
为直径的⊙ ,并标出⊙
,并标出⊙ 的交点
的交点 ,与
,与 的交点
的交点 (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法). ;
; 的周长.
的周长. 的一元二次方程:
的一元二次方程: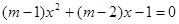 (
( 为实数).
为实数).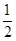 是此方程的实数根,抛物线
是此方程的实数根,抛物线 与
与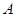 、
、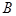 ,抛物线的顶点为
,抛物线的顶点为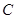 ,
,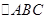 的面积.
的面积. 的图象的两个交点.
的图象的两个交点.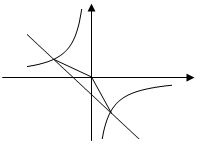
 到直线AB的距离.
到直线AB的距离. 粤公网安备 44130202000953号
粤公网安备 44130202000953号