设三组实验数据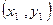 .
.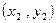 .
.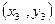 的回归直线方程是:
的回归直线方程是: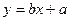 ,使代数式
,使代数式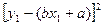
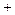
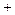
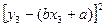 的值最小时,
的值最小时,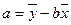 ,
,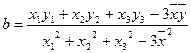 ,(
,(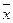 、
、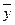 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如下:
| x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
6 |
5 |
6.2 |
8 |
7.1 |
8.6 |
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若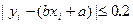 ,即称
,即称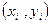 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
推荐套卷
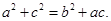
 ,求函数
,求函数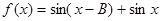 的值域。
的值域。 上有意义的两个函数
上有意义的两个函数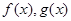 ,如果对于任意的
,如果对于任意的 ,都有
,都有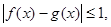 则称
则称 给定一个区间
给定一个区间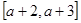 。
。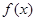 在区间
在区间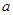 的取值范围;
的取值范围;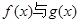 在区间
在区间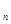 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且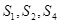 成等比数列。
成等比数列。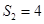 ,求
,求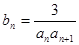 ,
, 是数列
是数列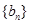 的前
的前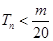 对所有
对所有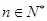 都成立的最小正整数
都成立的最小正整数 。
。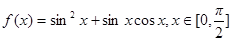
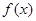 的值域;
的值域; ,求
,求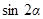 的值。
的值。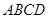 中,已知
中,已知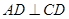 ,
,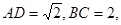
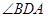 =60°,
=60°, =135°,求
=135°,求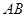 的长。
的长。 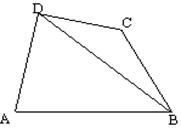
 粤公网安备 44130202000953号
粤公网安备 44130202000953号