（本小题满分10分）某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为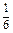
.甲、乙、丙三位同学每人购买了一瓶该饮料。
（Ⅰ）求三位同学都没有中奖的概率；
（Ⅱ）求三位同学中至少有两位没有中奖的概率.
，
，若
，求实数
的值.
的前4项和为10，且
成等比数列，
是各项均为正数的等比数列，
，
。
的第10项为23，第25项为
，求：
中，已知
求
和
。推荐套卷
（本小题满分10分）某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为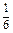.甲、乙、丙三位同学每人购买了一瓶该饮料。
（Ⅰ）求三位同学都没有中奖的概率；
（Ⅱ）求三位同学中至少有两位没有中奖的概率.
粤公网安备 44130202000953号