统计某校100名学生的数学会考成绩，得到样本频率分布直方图如右图示，规定不低于60分为及格，不低于85分为优秀，
（1）估计这次考试的及格人数和优秀率；
（ 2）从成绩是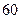
分以下（包括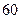分）的学生中选两人，求他们不在同一分数段的概率.
 |
相关试题
，
.
的单调区间和最值；
在
上的函数
的图像关于直线
对称，当
时，
的图像如图所示.
的解.
，求函数
的最大值和最小值.
：
的值；
上存在零点，求实数
.
的定义域；
在第一象限且
，求
的值.推荐套卷
统计某校100名学生的数学会考成绩，得到样本频率分布直方图如右图示，规定不低于60分为及格，不低于85分为优秀，
（1）估计这次考试的及格人数和优秀率；
（ 2）从成绩是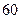分以下（包括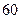分）的学生中选两人，求他们不在同一分数段的概率.
|
粤公网安备 44130202000953号