（本小题满分12分）学习小组有6个同学，其中4个同学从来没有参加过数学研究性学习活动，2个同学曾经参加过数学研究性学习活动.
（1）现从该小组中任选2个同学参加数学研究性学习活动，求恰好选到1个曾经参加过数学研究性学习活动的同学的概率；
（2）若从该小组中任选2个同学参加数学研究性学习活动，活动结束后，该小组没有参加过数学研究性学习活动的同学个数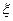
是一个随机变量，求随机变量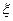的分布列及数学期望
.
的解析式；
，求函数
的最大值和最小值以及对应的
值；
，
恒成立，求实数
的取值范围
的值； 
的值
的定义域；
时，函数
，求实数
的值
为钝角，且
，求
.
，求
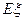的值推荐套卷
（本小题满分12分）学习小组有6个同学，其中4个同学从来没有参加过数学研究性学习活动，2个同学曾经参加过数学研究性学习活动.
（1）现从该小组中任选2个同学参加数学研究性学习活动，求恰好选到1个曾经参加过数学研究性学习活动的同学的概率；
（2）若从该小组中任选2个同学参加数学研究性学习活动，活动结束后，该小组没有参加过数学研究性学习活动的同学个数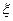是一个随机变量，求随机变量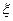的分布列及数学期望.
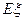粤公网安备 44130202000953号