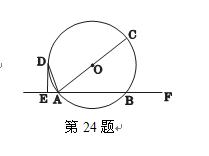
已知△ABC,分别以AC和BC为直径作半圆O1,O2,P是AB的中点,
(1)如图1,若△ABC是等腰三角形,且AC=BC,在 ,
, 上分别取点E、F,使∠AO1E=∠BO2F
上分别取点E、F,使∠AO1E=∠BO2F ,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;
,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;
(2)如图2,若(1)中△ABC是任意三角形,其他条件不变,则(1)中的两个结论还成立吗?若成立,请给出证明;
(3)如图3,若PC是⊙O1的切线,求证:AB2=BC2+3AC2.
相关知识点
推荐套卷
 在抛物线
在抛物线 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线 相交于点
相交于点 ,连接
,连接 ,设点
,设点 ,且
,且 .
.
 时,求点
时,求点 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直; 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
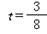 (小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度; 上建有一座电信信号发射架
上建有一座电信信号发射架 ,现在山脚
,现在山脚 处测得峰顶的仰角为
处测得峰顶的仰角为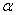 ,发射架顶端的仰角为
,发射架顶端的仰角为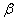 ,其中
,其中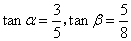 ,求发射架高
,求发射架高
 粤公网安备 44130202000953号
粤公网安备 44130202000953号