本题满分13分
如图，三角形ABC中，AC=BC=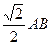
，ABED是边长为1
的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．
（I）求证：GF//底面ABC；
（Ⅱ）求证：AC⊥平面EBC；
（Ⅲ）求几何体ADEBC的体积V．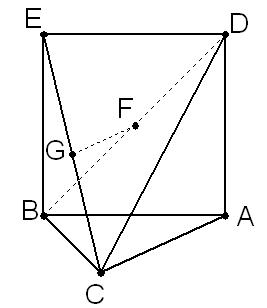
相关试题
的圆柱形水池，已知底的单位面积造价是侧面单位造价的一半，问：如何设计水池的底半径和高，才能使总造价最省？
长的墙壁，问应围成怎样的长方形才能使这间小屋的面积最大？
个相同的矩形鱼池，每个面积为
，鱼池前面要留
宽的运料通道，其余各边为
宽的堤埂，问：每个鱼池的长宽各多少米时，占地面积最少。
的矩形板的四个角上截去四个相同的小正方形，作成一个无盖的盒子，求盒子容积的最大值。
为函数
的边际函数，某企业每月最多生产
台报警器，已知每生产
台的收入函数为
（单位：元），其成本函数为
（单位：元），利润是收入与成本的差。（1）求利润函数
及其边际函数
；（2）利润函数推荐套卷
本题满分13分如图，三角形ABC中，AC=BC=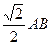，ABED是边长为1
的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．
（I）求证：GF//底面ABC；
（Ⅱ）求证：AC⊥平面EBC；
（Ⅲ）求几何体ADEBC的体积V．
粤公网安备 44130202000953号