设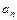 =1+
=1+ +
+ +…+
+…+ (n
(n ),
),
(1)分别求出满足 +
+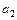 +…+
+…+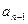 =g(n)(
=g(n)(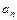 -1)的
-1)的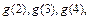 并猜想
并猜想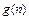 的表达式;
的表达式;
(2)用数学归纳法证明:(1)中猜想所得的g(n)使得等式 +
+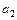 +…+
+…+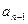 =g(n)(
=g(n)(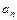 -1)对于大于1的一切自然数n都成立。
-1)对于大于1的一切自然数n都成立。
推荐套卷
设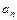 =1+
=1+ +
+ +…+
+…+ (n
(n ),
),
(1)分别求出满足 +
+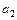 +…+
+…+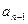 =g(n)(
=g(n)(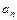 -1)的
-1)的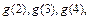 并猜想
并猜想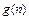 的表达式;
的表达式;
(2)用数学归纳法证明:(1)中猜想所得的g(n)使得等式 +
+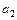 +…+
+…+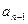 =g(n)(
=g(n)(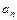 -1)对于大于1的一切自然数n都成立。
-1)对于大于1的一切自然数n都成立。