已知圆M：（x+1）2+y2=8，定点N（1，0），点P为圆M上的动点，若Q在NP上，点G在MP上，且满足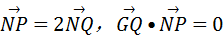
．
（I）求点G的轨迹C的方程；
（II）直线l过点P（0，2）且与曲线C相交于A、B两点，当△AOB面积取得最大值时，求直线l的方程．
.
的值
，求：
的最小正周期；（Ⅱ）
.
ABC中的两条角平分线
和
相交于
，
B=60
，
在
上，且
。
四点共圆；推荐套卷
已知圆M：（x+1）2+y2=8，定点N（1，0），点P为圆M上的动点，若Q在NP上，点G在MP上，且满足．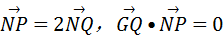
（I）求点G的轨迹C的方程；
（II）直线l过点P（0，2）且与曲线C相交于A、B两点，当△AOB面积取得最大值时，求直线l的方程．
粤公网安备 44130202000953号