如图，抛物线y＝ax2－4ax＋c（a≠0）经过A（0，－1），B（5，0）两点，点P是抛物线上的一个动点
，且位于直线AB的下方（不与A，B重合），过点P作直线PQ⊥x轴，交AB于点Q，设点P的横坐标为m．
（1）求a，c的值；
（2）设PQ的长为S，求S与m的函数关系式，写出m的取值范围；
（3）以PQ为直径的圆与抛物线的对称轴l有哪些位置关系？并写出对应的m取值范围．（不必写过程）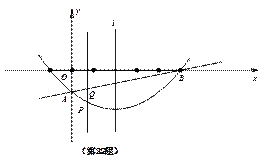
相关试题
观察下图，回答下列问题：
（1）在图①中有几个角？
（2）在图②中有几个角？
（3）在图③中有几个角？
（4）以此类推，如图④所示，若一个角内有n条射线，此时共有多少个角？
（1）已知∠AOB是直角，OM平分∠AOC，ON平分∠BOC，求∠MON与∠AOB的关系．
（2）如果（1）中，改变∠AOB的大小，其他条件不变，求∠MON与∠AOB的关系．
（3）你从（1），（2）的结果中能发现什么规律？
OE ,OF 平分∠AOE, ∠COF=34°,求∠BOD的度数.
已知A、B两家商店的随身听的单价相同，书包的单价也相同，随身听和书包的单价之和为452元，且随身听的单价比书包的单价的4倍少8元．
(1)问随身听和书包的单价各是多少元?
(2)现在这两家商店搞促销，促销方式如下：
商店A：所有的商品打八折销售；
商店B：每购物满100元，立即返还25元(例如，购物205元，则立即返还50元)．
小明身上带了400元钱，想买随身听和书包各一个，那么，他应该选择在哪一家商店购买更省钱?
相关知识点
推荐套卷
粤公网安备 44130202000953号