(本小题满分12分) 月份,有一款新服装投入某市场销售,
月份,有一款新服装投入某市场销售, 月
月 日该款服装
日该款服装
仅销售出 件,
件, 月
月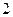 日售出
日售出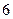 件,
件, 月
月 日售出
日售出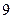 件,
件, 月
月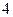 日售出
日售出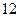 件,尔后,每天售
件,尔后,每天售
出的件数分别递增 件,直到日销售量达到最大(只有
件,直到日销售量达到最大(只有 天)后,每天销售的件数开始下降,
天)后,每天销售的件数开始下降,
分别递减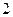 件,到
件,到 月
月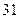 日刚好售出
日刚好售出 件.
件.
(Ⅰ)问 月几号该款
月几号该款 服装销售件数最多?其最大值是多少?
服装销售件数最多?其最大值是多少?
(Ⅱ)按规律,当该商场销售此服装达到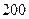 件时,社会上就开始流行,而日销售量连续下降
件时,社会上就开始流行,而日销售量连续下降
并低于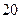 件时,则不再流行,问该款服装在社会上流行几天?说明理由.
件时,则不再流行,问该款服装在社会上流行几天?说明理由.
推荐套卷
(本小题满分12分) 月份,有一款新服装投入某市场销售,
月份,有一款新服装投入某市场销售, 月
月 日该款服装
日该款服装
仅销售出 件,
件, 月
月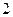 日售出
日售出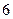 件,
件, 月
月 日售出
日售出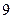 件,
件, 月
月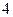 日售出
日售出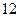 件,尔后,每天售
件,尔后,每天售
出的件数分别递增 件,直到日销售量达到最大(只有
件,直到日销售量达到最大(只有 天)后,每天销售的件数开始下降,
天)后,每天销售的件数开始下降,
分别递减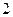 件,到
件,到 月
月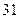 日刚好售出
日刚好售出 件.
件.
(Ⅰ)问 月几号该款
月几号该款 服装销售件数最多?其最大值是多少?
服装销售件数最多?其最大值是多少?
(Ⅱ)按规律,当该商场销售此服装达到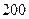 件时,社会上就开始流行,而日销售量连续下降
件时,社会上就开始流行,而日销售量连续下降
并低于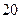 件时,则不再流行,问该款服装在社会上流行几天?说明理由.
件时,则不再流行,问该款服装在社会上流行几天?说明理由.