根据国务院新闻办公室2011年4月28日发布的《2011年全国第六次人口普查主要数据公报(第1号)》,就全国人口受教育情况的数据绘制了条形统计图和扇形统计图如下: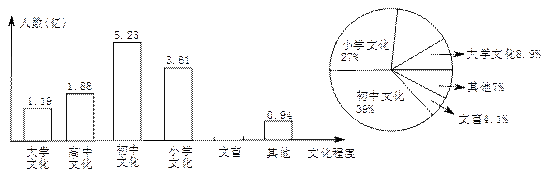
根据统计图提供的信息,解答下列问题:
(1)这次人口普查统计的全国人口总数约为 亿人(精确到0.1)
(2)补全条条形统计图和扇形统计图
(3)求扇形统计图中表示“高中文化”的圆心角的度数
根据国务院新闻办公室2011年4月28日发布的《2011年全国第六次人口普查主要数据公报(第1号)》,就全国人口受教育情况的数据绘制了条形统计图和扇形统计图如下: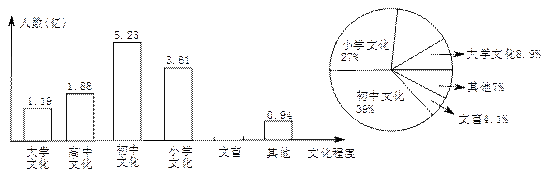
根据统计图提供的信息,解答下列问题:
(1)这次人口普查统计的全国人口总数约为 亿人(精确到0.1)
(2)补全条条形统计图和扇形统计图
(3)求扇形统计图中表示“高中文化”的圆心角的度数