某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓是单价为40元，设第二个月单价降低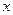
元．
（1）填表：（不需化简）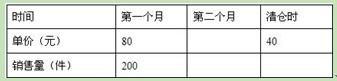
（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？
相关试题
某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓是单价为40元，设第二个月单价降低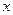元．
（1）填表：（不需化简）
（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？
中，
∥
，点
在
上，连接
并延长与
．
∽△
； 
∥
于点
，若
，求
是
上一点，
∥
，
分别交
于点
，∠1=∠2，探索线段
之间的关系，并说明理由.
中，
，
平分∠
∥
．求证：
．
中，
为边
延长线上的一点，且
为
的黄金分割点，即
，
交
于点
，已知
，求
的长．
中，
，垂足为
，
是
的平分线，
，垂足为
.
为矩形.
粤公网安备 44130202000953号