(本小题满分14分)
已知函数f(x)=－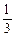
x3+bx2+cx+bc，
(1)若函数f(x)在x=1处有极值－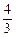
，试确定b、c的值；
(2)在(1)的条件下，曲线y=f(x)+m与x轴仅有一个交点，求实数m的取值范围；
(3)记g(x)=|f′( x)|(－1≤x≤1)的最大值为M，若M≥k对任意的b、c恒成立，试求k的取值范围．
(参考公式：x3－3bx2+4b3=(x+b)(x－2b)2)
轴和
轴上，其长度分别为８和６，
为何值时，直线
．
；（2）在
轴上的截距为１．
，直线
，求：
且与
平行的直线的方程；
，
，
求直线
，
，
的斜率，并判断这些直线的倾斜角是锐角还是钝角．
，
，
，
为顶点的四边形的形状，并说明理由．推荐套卷
(本小题满分14分)
已知函数f(x)=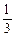－x3+bx2+cx+bc，
(1)若函数f(x)在x=1处有极值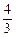－，试确定b、c的值；
(2)在(1)的条件下，曲线y=f(x)+m与x轴仅有一个交点，求实数m的取值范围；
(3)记g(x)=|f′( x)|(－1≤x≤1)的最大值为M，若M≥k对任意的b、c恒成立，试求k的取值范围．
(参考公式：x3－3bx2+4b3=(x+b)(x－2b)2)
粤公网安备 44130202000953号