设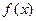
是定义域在
上的奇函数，且其图象上任意两点连线的斜率均小于零.
（l）求证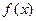在上是减函数；
（ll）如果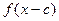
，
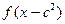的定义域的交集为空集，求实数
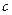的取值范围；
（lll）证明若
，则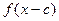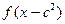，存在公共的定义域，并求这个公共的空义域.
，集合
，
；
，求
的值。
，
，
满足
，
求实数
的值。
,其中
,如果
，求实数
的取值范围。
，
，
推荐套卷
设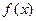是定义域在上的奇函数，且其图象上任意两点连线的斜率均小于零.
（l）求证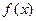在上是减函数；
（ll）如果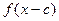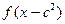，的定义域的交集为空集，求实数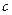的取值范围；
（lll）证明若，则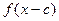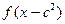，存在公共的定义域，并求这个公共的空义域.
粤公网安备 44130202000953号