如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB的延长线于点G.
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求 的值.
的值.
相关知识点
推荐套卷



 ,
, ,2各数和它们的相反数在数轴上表示出来,并比较它们的大小,用“<”号连接。
,2各数和它们的相反数在数轴上表示出来,并比较它们的大小,用“<”号连接。 ,
,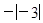 ,
,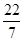 ,-0.3,1.7,
,-0.3,1.7, ,0 , 1.1010010001……(每两个1之间依次多一个0)
,0 , 1.1010010001……(每两个1之间依次多一个0) 粤公网安备 44130202000953号
粤公网安备 44130202000953号