(本小题满分12分)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,……,依次类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是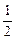 .记小球遇到第
.记小球遇到第 行第
行第 个障碍物(从左至右)上顶点的概率为
个障碍物(从左至右)上顶点的概率为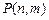 .
.
(Ⅰ)求 ,
, 的值,并猜想
的值,并猜想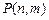 的表达式(不必证明);
的表达式(不必证明);
(Ⅱ)已知 ,设小球遇到第6行第
,设小球遇到第6行第 个障碍物(从左至右)上顶点时,
个障碍物(从左至右)上顶点时,
得到的分数为 ,试求
,试求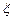 的分布列及数学期望.
的分布列及数学期望.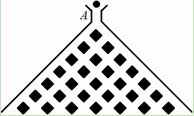
推荐套卷
 ,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。
,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。 :
: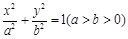 的离心率为
的离心率为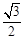 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线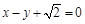 相切.
相切. ,
,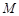 、
、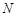 是椭圆
是椭圆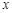 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结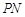 交椭圆
交椭圆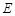 ,求直线
,求直线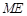 与
与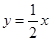 上时,求直线AB的方程.
上时,求直线AB的方程.
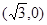
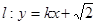 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号