如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=-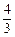 x+
x+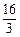 ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
(3)当t为何值时s有最大值?并求出最大值.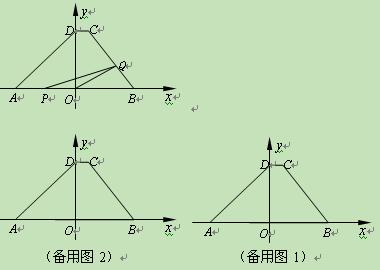
相关知识点
推荐套卷

 划购进电视机和洗衣机共100台,商店最多可筹集资金160 800元.
划购进电视机和洗衣机共100台,商店最多可筹集资金160 800元. 获得利润最多?并求出最多利润.(利润=售价-进价)
获得利润最多?并求出最多利润.(利润=售价-进价) 机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附某校八年级女生立定跳远的计分标准)
机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附某校八年级女生立定跳远的计分标准)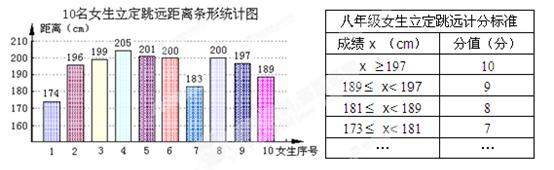
 中,
中,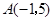 ,
,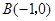 ,
,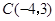 .
.
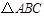 的面积.
的面积.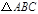 关于
关于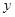 轴的轴对称图形
轴的轴对称图形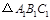 .
. 的坐标.
的坐标.
 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号