(本题8分)某校八年级200名女生在体育测试中进行了立定跳远的测试.现从200名女生中随
机抽取10名女生进行测试，下面是她们测试结果的条形统计图.（另附某校八年级女生立定跳远的计分标准）
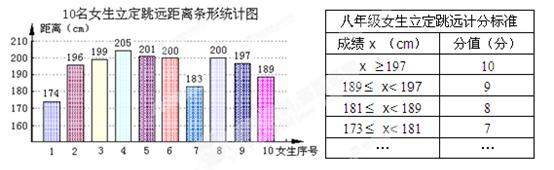
（1）求这10名女生立定跳远距离的中位数，立定跳远得分的众数和平均数.
（2）请你估计该校200名女生在立定跳远测试中得10分的人数.
(本题8分)某校八年级200名女生在体育测试中进行了立定跳远的测试.现从200名女生中随机抽取10名女生进行测试，下面是她们测试结果的条形统计图.（另附某校八年级女生立定跳远的计分标准）（1）求这10名女生立定跳远距离的中位数，立定跳远得分的众数和平均数.
（2）请你估计该校200名女生在立定跳远测试中得10分的人数.
个A种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B种造形需甲种花卉50盆，乙种花卉90盆。你班承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来。
粤公网安备 44130202000953号