如图,已知反比例函数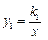 (k1>0)与一次函数
(k1>0)与一次函数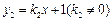 相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?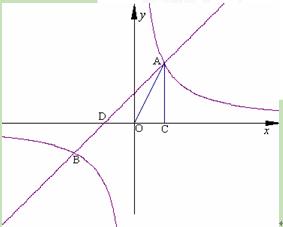
推荐套卷
如图,已知反比例函数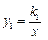 (k1>0)与一次函数
(k1>0)与一次函数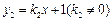 相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?