如图，已知三棱柱ABC－A1B1C1中，侧棱A A1⊥底面ABC
AB⊥BC；
（Ⅰ）求证：平面A1BC⊥侧面A1ABB1.
（Ⅱ）若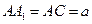
,直线AC与平面A1BC所成的角为
，
求AB的长。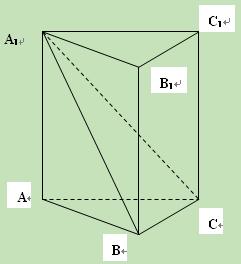
相关试题
的焦距为2c，直线
过点（
，0）和（0，
），且点（1，0）到直线
求双曲线的离心率e的取值范围.
，问是否存在斜率为1的直线
，使
的极坐标方程为
，圆C的参数方程为
，求直线已知函数
在点
处取得极值。
（1）求实数a的值；
（2）若关于x的方程
在区间[0，2]上有两个不等实根，求b的取值范围；
（3）证明：对于任意的正整数
，不等式
。
，它的一个顶点恰好是抛物线
的焦点。
的值。推荐套卷
如图，已知三棱柱ABC－A1B1C1中，侧棱A A1⊥底面ABC
AB⊥BC；
（Ⅰ）求证：平面A1BC⊥侧面A1ABB1.
（Ⅱ）若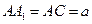,直线AC与平面A1BC所成的角为，
求AB的长。
已知函数在点处取得极值。
（1）求实数a的值；
（2）若关于x的方程在区间[0，2]上有两个不等实根，求b的取值范围；
（3）证明：对于任意的正整数，不等式。
粤公网安备 44130202000953号