.
（1）
人坐在有八个座位的一排上，若每人的左右两边都要有空位，则不同的坐法的种数为几种？
（2）甲、乙、丙人站在共有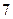
级的台阶上，若每级台阶最多站
人，同一级台阶上
不区分站的位置，则有多少种不同的站法？
（3）现有
个保送大学的名额，分配给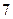所学校，每校
至少
个名额，问名额分配的方法共有多少种？
相关试题
中，角A、B、C的对边分别为
，已知向量
且满足
，（1）求角A的大小；
试判断
，点N在AC上，且AN＝2NC，AM与BN相交于点P，AP=λAM，求(1)λ的值 (2)
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求
；(2)求|a＋b|的最大值
,
,当
为何值时，
与
垂直？（2）
与
推荐套卷
.
（1）人坐在有八个座位的一排上，若每人的左右两边都要有空位，则不同的坐法的种数为几种？
（2）甲、乙、丙人站在共有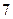级的台阶上，若每级台阶最多站人，同一级台阶上
不区分站的位置，则有多少种不同的站法？
（3）现有个保送大学的名额，分配给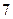所学校，每校至少个名额，问名额分配的方法共有多少种？
粤公网安备 44130202000953号