对于函数 ,若存在
,若存在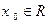 ,使得
,使得 成立,称
成立,称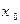 为不动点,已知函数
为不动点,已知函数
(1) 当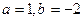 时,求函数
时,求函数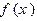 不动点;
不动点;
(2) 若对任意的实数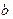 ,函数
,函数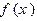 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(3) 在(2)的条件下,若 图象上A,B两点的横坐标是函数
图象上A,B两点的横坐标是函数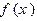 不动点,且
不动点,且 两点关于直线
两点关于直线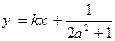 对称,求b的最小值.
对称,求b的最小值.
推荐套卷
对于函数 ,若存在
,若存在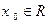 ,使得
,使得 成立,称
成立,称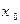 为不动点,已知函数
为不动点,已知函数
(1) 当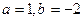 时,求函数
时,求函数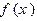 不动点;
不动点;
(2) 若对任意的实数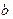 ,函数
,函数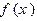 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(3) 在(2)的条件下,若 图象上A,B两点的横坐标是函数
图象上A,B两点的横坐标是函数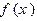 不动点,且
不动点,且 两点关于直线
两点关于直线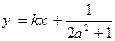 对称,求b的最小值.
对称,求b的最小值.