下表是关于某设备的使用年限（年）和所需要的维修费用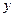
(万元)的几组统计数据：
 |
2 |
3 |
4 |
5 |
6 |
|
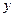2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
（1）请在给出的坐标系中画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出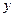关于的线性回归方程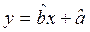
；
（3）估计使用年限为10年时，维修费用为多少？
(参考数值：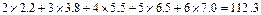
)
；
，x0=2；
，x0=1.
在x=x0处的导数.
x3+
.推荐套卷
下表是关于某设备的使用年限（年）和所需要的维修费用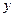(万元)的几组统计数据：
|
2 |
3 |
4 |
5 |
6 |
|
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
（1）请在给出的坐标系中画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出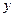关于的线性回归方程；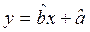
（3）估计使用年限为10年时，维修费用为多少？
(参考数值：)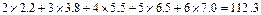
粤公网安备 44130202000953号