如图,已知斜三棱柱 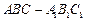 的底面是直角三角形,
的底面是直角三角形,  ,侧棱与底面所成的角为
,侧棱与底面所成的角为  ,点
,点  在底面上的射影
在底面上的射影  落在
落在  上.
上.

(1)若点  恰为
恰为  的中点,且
的中点,且  ,求
,求 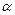 的值.
的值.
(2)若  ,且当
,且当 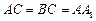 时,求二面角
时,求二面角 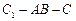 的大小.
的大小.
推荐套卷
如图,已知斜三棱柱 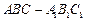 的底面是直角三角形,
的底面是直角三角形,  ,侧棱与底面所成的角为
,侧棱与底面所成的角为  ,点
,点  在底面上的射影
在底面上的射影  落在
落在  上.
上.

(1)若点  恰为
恰为  的中点,且
的中点,且  ,求
,求 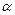 的值.
的值.
(2)若  ,且当
,且当 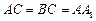 时,求二面角
时,求二面角 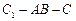 的大小.
的大小.