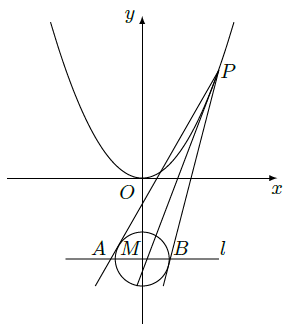
如图,设
是抛物线
:
上动点。圆
:
的圆心为点
,过点
做圆
的两条切线,交直线
:
于
两点。(Ⅰ)求
的圆心
到抛物线
准线的距离。
(Ⅱ)是否存在点
,使线段
被抛物线
在点
处得切线平分,若存在,求出点
的坐标;若不存在,请说明理由.
推荐套卷
如图,设
是抛物线
:
上动点。圆
:
的圆心为点
,过点
做圆
的两条切线,交直线
:
于
两点。(Ⅰ)求
的圆心
到抛物线
准线的距离。
(Ⅱ)是否存在点
,使线段
被抛物线
在点
处得切线平分,若存在,求出点
的坐标;若不存在,请说明理由.
