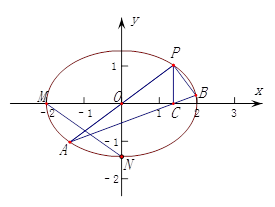
如图,在平面直角坐标系
中,
分别是椭圆
的顶点,过坐标原点的直线交椭圆于
两点,其中
在第一象限.过
作
轴的垂线,垂足为
.连接
,并延长交椭圆于点
.设直线
的斜率为
.
(Ⅰ)当直线
平分线段
时,求
的值;
(Ⅱ)当
时,求点
到直线
的距离;
(Ⅲ)对任意
,求证:
.
推荐套卷
如图,在平面直角坐标系
中,
分别是椭圆
的顶点,过坐标原点的直线交椭圆于
两点,其中
在第一象限.过
作
轴的垂线,垂足为
.连接
,并延长交椭圆于点
.设直线
的斜率为
.

(Ⅰ)当直线
平分线段
时,求
的值;
(Ⅱ)当
时,求点
到直线
的距离;
(Ⅲ)对任意
,求证:
.