(本小题满分12分)如图，正三角形ABC与直角三角形BCD成直二面角，且∠BCD=90°，∠CBD=30°.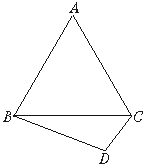
(1)求证：AB⊥CD；
(2)求二面角D—AB—C的大小；
(3)求异面直线AC和BD所成的角.
相关试题
中，
，点
分别在
上，且
，现将梯形
折起，使平面
与平面
垂直(如图②)．
平面
；
时，求二面角
的大小．
中，
，点
是
的中点.
；
平面
；
与
所成角的余弦值.
的底面是正方形，
，点
在棱
上.
；
且
体积.
中，
，
，
.
；
的正切值. 
中，
，
是
和
的中点.（Ⅰ）求证：
平面
;
,求
推荐套卷
(本小题满分12分)如图，正三角形ABC与直角三角形BCD成直二面角，且∠BCD=90°，∠CBD=30°.
(1)求证：AB⊥CD；
(2)求二面角D—AB—C的大小；
(3)求异面直线AC和BD所成的角.
粤公网安备 44130202000953号