（本小题满分12分）
设函数f (x)=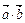
，其中向量
=(
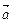cosx＋1，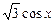
)，
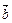=(cosx－1，2sinx)，x∈R．（Ⅰ）求f (x)的解析式；（Ⅱ）求f (x)的最小正周期、对称轴方程和对称中心的坐标。
作直线
，使它与两坐标轴相交且与两轴所围成的三角形面积为
．
并且在两个坐标轴上的截距的绝对值相等的直线有几条？请求出这些直线的方程。
的交点且平行于直线
的直线方程。
为直线
上一点，证明：这条直线的方程可以写成
．
和
轴，
轴分别交于点
，在线段
为边在第一象限内作等边△
，如果在第一象限内有一点
使得△
和△
的值。相关知识点
推荐套卷
（本小题满分12分）
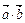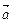设函数f (x)=，其中向量=(cosx＋1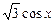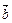，)， =(cosx－1，2sinx)，x∈R．（Ⅰ）求f (x)的解析式；（Ⅱ）求f (x)的最小正周期、对称轴方程和对称中心的坐标。
粤公网安备 44130202000953号