(本小题满分12分)
新能源汽车是指除汽油、柴油发动机之外所有其它能源汽车.包括燃料电池汽车、混合动力汽车、氢能源动力汽车和太阳能汽车等.其废气排放量比较低.为了配合我国“节能减排”战略,某汽车厂决定转型生产新能源汽车中的燃料电池汽车、混合动力和氢能源动力三类轿车,每类轿车均有标准型和豪华型两种型号,某月的产量如下表(单位:辆):
|
燃料电池轿车
|
混合动力轿车
|
氢能源动力轿车
|
标准型
|
100
|
200
|
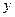
|
豪华型
|
200
|
300
|
500
|
按类型分层抽样的方法在这个月生产的轿车中抽取100辆,其中有燃料电池轿车20辆.
(I) 求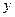 的值.
的值.
(II) 用分层抽样的方法在氢能源动力轿车中抽取一个容量为7的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆标准型轿车的概率;
(Ⅲ) 用随机抽样的方法从混合动力标准型轿车中抽取10辆,经检测它们的得分如下:
9.3, 8.7, 9.1, 9.5, 8.8, 9.4, 9.0, 8.2,9.6, 8.4.
把这10辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.4的概率.