(本小题满分12分)在一次食品卫生大检查中,执法人员从抽样中得知,目前投放我市的甲、乙两种食品的合格率分别为 和
和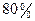 .
.
(1)今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
(2)若某消费者从两种食品中任意各购一件,设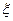 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出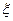
的分布列,并求其数学期望.
推荐套卷
(本小题满分12分)在一次食品卫生大检查中,执法人员从抽样中得知,目前投放我市的甲、乙两种食品的合格率分别为 和
和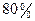 .
.
(1)今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
(2)若某消费者从两种食品中任意各购一件,设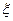 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出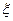
的分布列,并求其数学期望.