(本小题满分12分)在平面直角坐标系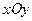 中,线段AB与y轴交于点
中,线段AB与y轴交于点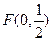 ,直线AB的斜率为k,且满足
,直线AB的斜率为k,且满足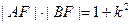
(1)证明:对任意的实数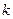 ,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
(2)对(1)中的抛物线C,若直线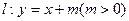 与其交于M、N两点,求∠MON的取值范围.
与其交于M、N两点,求∠MON的取值范围.
推荐套卷
(本小题满分12分)在平面直角坐标系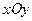 中,线段AB与y轴交于点
中,线段AB与y轴交于点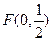 ,直线AB的斜率为k,且满足
,直线AB的斜率为k,且满足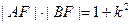
(1)证明:对任意的实数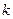 ,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
(2)对(1)中的抛物线C,若直线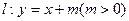 与其交于M、N两点,求∠MON的取值范围.
与其交于M、N两点,求∠MON的取值范围.