（本小题满分14分）已知各项均不为零的数列{an}的前n项和为Sn，且满足a1＝c，
2Sn＝an an＋1＋r．
（1）若r＝－6，数列{an}能否成为等差数列？若能，求
满足的条件；若不能，请说明理由；
（2）设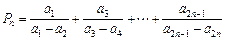
，
，
若r＞c＞4，求证：对于一切n∈N*，不等式
恒成立．
相关试题
所表示的平面区域为
，记
.
、
、
的值及
的表达式；
，
为
的前
项和，求
,cosB=
, 试判断三角形的形状．推荐套卷
（本小题满分14分）已知各项均不为零的数列{an}的前n项和为Sn，且满足a1＝c，
2Sn＝an an＋1＋r．
（1）若r＝－6，数列{an}能否成为等差数列？若能，求满足的条件；若不能，请说明理由；
（2）设，，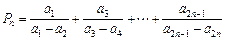
若r＞c＞4，求证：对于一切n∈N*，不等式恒成立．
粤公网安备 44130202000953号