（本小题满分12分）甲有一个装有
个红球、
个黑球的箱子，乙有一个装有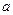
个红球、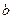
个黑球的箱子，两人各自从自己的箱子里任取一球，并约定:所取两球同色时甲胜，异色时乙胜（，，，
）．
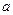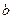(Ⅰ)当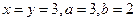
,时，求甲获胜的概率；
（Ⅱ）当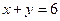
，
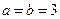时，规定：甲取红球获胜得3分；取黑球获胜得1分；甲负得0分．求甲的得分期望达到最大时的，值；
（Ⅲ）当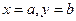
时，这个游戏规则公平吗？请说明理由．
相关试题
中，
，求数列
的前
项和
．
是公比为正数的等比数列，
，
是首项为1，公差为2的等差数列，求数列
的前
项和
．
，求函数
的最大值；
，且
，求
的最小值．
满足
为等比数列；
，问：数列
，使
的对边分别为
，且
；
，
，求
及
的值。推荐套卷
（本小题满分12分）甲有一个装有个红球、个黑球的箱子，乙有一个装有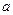个红球、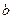个黑球的箱子，两人各自从自己的箱子里任取一球，并约定:所取两球同色时甲胜，异色时乙胜（，，，）．
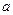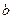(Ⅰ)当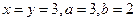,时，求甲获胜的概率；
（Ⅱ）当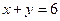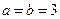，时，规定：甲取红球获胜得3分；取黑球获胜得1分；甲负得0分．求甲的得分期望达到最大时的，值；
（Ⅲ）当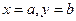时，这个游戏规则公平吗？请说明理由．
粤公网安备 44130202000953号