(本小题满分12分)
计算机考试分理论考试与上机操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中合格的概率分别为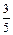 ,
,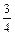 ,
,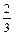 ;在上机操作考试中合格的概率分别为
;在上机操作考试中合格的概率分别为 ,
,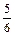 ,
,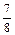 .所有考试是否合格相互之间没有影响.
.所有考试是否合格相互之间没有影响.
(Ⅰ)甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大?
(Ⅱ)求这三人计算机考试都获得“合格证书”的概率;
(Ⅲ)用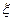 表示甲、乙、丙三人在理论考核中合格人数,求
表示甲、乙、丙三人在理论考核中合格人数,求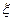 的分布列和数学期望
的分布列和数学期望 .
.
推荐套卷
 每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足R(x)=
每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足R(x)=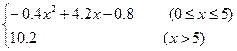 .假定该产品销售平衡,那么根据上述统计规律.
.假定该产品销售平衡,那么根据上述统计规律. 在
在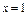 处取得极值。
处取得极值。 的值;
的值; 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数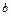 的取值范围;
的取值范围;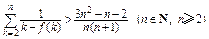 。参考数据:
。参考数据: 。
。 满足
满足 ,且
,且 。
。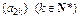 为等比数列;(2)求数列
为等比数列;(2)求数列 为非零常数)。试确定
为非零常数)。试确定 的值,使得对任意
的值,使得对任意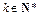 都有
都有 成立。
成立。 。当
。当 时,函数
时,函数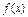 的取值范围恰为
的取值范围恰为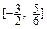 。
。 ,解关于
,解关于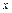 的不等式
的不等式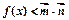 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号