列方程解应用题(10分)
某 单位组织职工旅游.下面是领队向旅行社导游咨询收费标准的一段对话:
单位组织职工旅游.下面是领队向旅行社导游咨询收费标准的一段对话:
领队:组团去“医巫闾山”旅游每人收费是多少?
导游:如果人数不超过25人,人均旅游费用为100元.
领队:超过25人怎样优惠呢?
导游:如果超过25人,每增加1人,人均旅游费用降低2元,但人均旅游费用不得低于70元.
该单位按旅行社的收费标准组团游览“医巫闾山”结束后,共支付给旅行社 2700元.
请你根据上述信息,求该单位这次到“医巫闾山”旅游的共有多少人?
相关知识点
推荐套卷

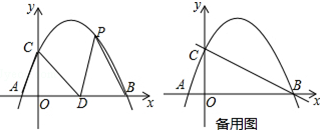

 AD,请给出证明;
AD,请给出证明;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号