已知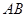 是半圆
是半圆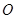 的直径, 点
的直径, 点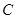 在
在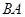 的延长线上运动(点
的延长线上运动(点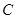 与点
与点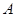 不重合), 以
不重合), 以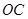 为直径的半圆
为直径的半圆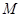 与半圆
与半圆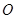 交于点
交于点 的平分线与半圆
的平分线与半圆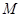 交于点
交于点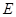 .
.
如图甲, 求证: 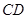 是半圆
是半圆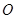 的切线;
的切线;
如图乙, 作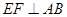 于点
于点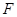 , 猜想
, 猜想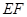 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;
如图丙, 在上述条件下, 过点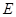 作
作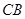 的平行线交
的平行线交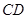 于点
于点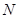 , 当
, 当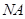 与半圆
与半圆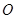 相切时, 求
相切时, 求
甲 乙 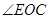 的正切值.
的正切值.
相关知识点
推荐套卷
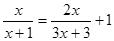
 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号