(本小题满分16分)
在直角坐标系xOy中,直线l与x轴正半轴和y轴正半轴分别相交于A,B两点,△AOB的内切圆为圆M.
(1)如果圆M的半径为1,l与圆M切于点C ( ,1+
,1+ ),求直线l的方程;
),求直线l的方程;
(2)如果圆M的半径为1,证明:当△AOB的面积、周长最小时,此时△AOB为同一个三角形;
(3)如果l的方程为x+y-2-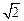 =0,P为圆M上任一点,求
=0,P为圆M上任一点,求 +
+ +
+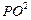 的最值.
的最值.
推荐套卷
(本小题满分16分)
在直角坐标系xOy中,直线l与x轴正半轴和y轴正半轴分别相交于A,B两点,△AOB的内切圆为圆M.
(1)如果圆M的半径为1,l与圆M切于点C ( ,1+
,1+ ),求直线l的方程;
),求直线l的方程;
(2)如果圆M的半径为1,证明:当△AOB的面积、周长最小时,此时△AOB为同一个三角形;
(3)如果l的方程为x+y-2-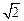 =0,P为圆M上任一点,求
=0,P为圆M上任一点,求 +
+ +
+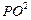 的最值.
的最值.