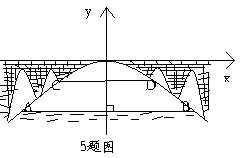
如图有一座抛物线形拱桥，桥下面在正常水位是AB宽20m，水位上升3m就达到警戒线CD，这是水面宽度为10m。
（1）在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？
.
相关试题
取何实数，多项式
的值都不会是正数．
，其中a＝－2，b＝3
，ab＝－2，求代数式
的值．
；
；
；
）＋3（－
÷（－3
）·（－
y）
）（相关知识点
推荐套卷
如图有一座抛物线形拱桥，桥下面在正常水位是AB宽20m，水位上升3m就达到警戒线CD，这是水面宽度为10m。
（1）在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？
.
粤公网安备 44130202000953号