设等比数列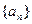 的前n项和为Sn,已知
的前n项和为Sn,已知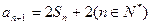
(1)求数列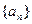 通项公式;
通项公式;
(2)在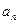 与
与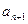 之间插入n个数,使这n+2个数组成一个公差为
之间插入n个数,使这n+2个数组成一个公差为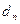 的等差数列。
的等差数列。
(Ⅰ)求证: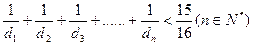
(Ⅱ)在数列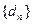 中是否存在三项
中是否存在三项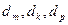 (其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
(其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
推荐套卷
设等比数列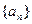 的前n项和为Sn,已知
的前n项和为Sn,已知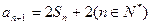
(1)求数列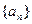 通项公式;
通项公式;
(2)在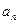 与
与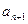 之间插入n个数,使这n+2个数组成一个公差为
之间插入n个数,使这n+2个数组成一个公差为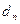 的等差数列。
的等差数列。
(Ⅰ)求证: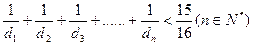
(Ⅱ)在数列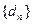 中是否存在三项
中是否存在三项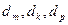 (其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
(其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由