在棱长为2的正方体ABCD—A1B1C1D1中，E，F分别为A1D1和CC1的中点．
（Ⅰ）求证：EF//平面ACD1；
（Ⅱ）求异面直线EF与AB所成的角的余弦值；
（Ⅲ）在棱BB1上是否存在一点P，使得二面角P—AC—B的大小为30°？若存在，求出BP的长；若不存在，请说明理由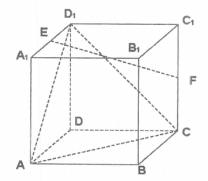
=
。若
。
（x∈R）的值域。
满足
为虚数单位），
，求一个以
为根的实系数一元二次方程.
.
的最小正周期是
，求函数
的值域以及单调递减区间。
，
（
是虚数单位），求
的最小值。推荐套卷
在棱长为2的正方体ABCD—A1B1C1D1中，E，F分别为A1D1和CC1的中点．
（Ⅰ）求证：EF//平面ACD1；
（Ⅱ）求异面直线EF与AB所成的角的余弦值；
（Ⅲ）在棱BB1上是否存在一点P，使得二面角P—AC—B的大小为30°？若存在，求出BP的长；若不存在，请说明理由
粤公网安备 44130202000953号