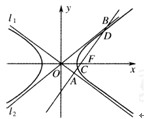
如图，双曲线的中心在坐标原点O，焦点在x轴上，两条渐近线分别为l1，l2，经过右焦点F垂直于l1的直线分别交l1，l2于A，B两点．又已知该双曲线的离心率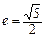
．
（1）求证：
，
，
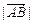依次成等差数列；
（2）若F(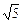
，0)，求直线AB在双曲线上所截得的弦CD的长度．
相关试题
，当
时取得极大值
，当
时取得极小值，求极小值及其对应的
的值。
，极大值为
，
的极值。
的单调区间与极值。
中，
且点
在直线
上.（1）求数列
的通项公式；（2）若函数
求函数
的最小值；（3）设
表示数列
的前项和．试问：是否存在关于
的整式
，使得
对于一切不小于2的自然数相关知识点
推荐套卷
如图，双曲线的中心在坐标原点O，焦点在x轴上，两条渐近线分别为l1，l2，经过右焦点F垂直于l1的直线分别交l1，l2于A，B两点．又已知该双曲线的离心率．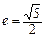
（1）求证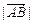：，，依次成等差数列；
（2）若F(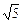，0)，求直线AB在双曲线上所截得的弦CD的长度．
粤公网安备 44130202000953号