（本小题满分12分）
如图
，已知四棱锥P—ABCD的底面是直角梯形，∠ABC＝∠BCD ＝90o，AB＝BC＝PB＝PC＝2CD＝2，侧面PBC⊥底面ABCD，O是BC的中点，AO交BD于E.
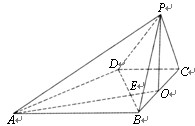
（1）求证：PA⊥BD；
（2）求二面角P—DC—B的
大小；
推荐套卷
（本小题满分12分）
如图，已知四棱锥P—ABCD的底面是直角梯形，∠ABC＝∠BCD ＝90o，AB＝BC＝PB＝PC＝2CD＝2，侧面PBC⊥底面ABCD，O是BC的中点，AO交BD于E.
（1）求证：PA⊥BD；
（2）求二面角P—DC—B的大小；
粤公网安备 44130202000953号