((本小题满分13分)
已知a>0,函数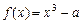 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线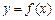 在点M(x1,
在点M(x1,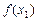 )处的切线为l.
)处的切线为l.
(1)求l的方程;
(2)设l与x轴的交点为(x2,0).证明:
①x2 ;②若x1
;②若x1 ,则
,则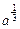 <x2<x1.
<x2<x1.
推荐套卷
((本小题满分13分)
已知a>0,函数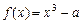 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线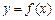 在点M(x1,
在点M(x1,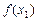 )处的切线为l.
)处的切线为l.
(1)求l的方程;
(2)设l与x轴的交点为(x2,0).证明:
①x2 ;②若x1
;②若x1 ,则
,则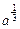 <x2<x1.
<x2<x1.