已知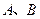 两地相距
两地相距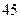 千米,
千米, 骑车人与客车分别从
骑车人与客车分别从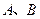 两地出发,往返于
两地出发,往返于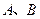 两地之间.下图中,折线表示某骑车人离开
两地之间.下图中,折线表示某骑车人离开 地的距离
地的距离 与时间
与时间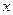 的函数关系.客车
的函数关系.客车 点从
点从 地出发,以
地出发,以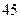 千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计)
千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计) 
① 在阅读下 图的基础上,直接回答:
图的基础上,直接回答: 骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
② 试问:骑车人何时与客车第二次相遇?(要求写 出演算过程).
出演算过程).
推荐套卷
已知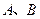 两地相距
两地相距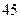 千米,
千米, 骑车人与客车分别从
骑车人与客车分别从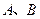 两地出发,往返于
两地出发,往返于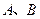 两地之间.下图中,折线表示某骑车人离开
两地之间.下图中,折线表示某骑车人离开 地的距离
地的距离 与时间
与时间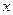 的函数关系.客车
的函数关系.客车 点从
点从 地出发,以
地出发,以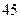 千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计)
千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计) 
① 在阅读下 图的基础上,直接回答:
图的基础上,直接回答: 骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
② 试问:骑车人何时与客车第二次相遇?(要求写 出演算过程).
出演算过程).