如图1,在平面内,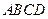 是
是 的矩形,
的矩形,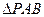 是正三角形,将
是正三角形,将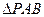 沿
沿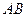 折起,使
折起,使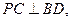 如图2,
如图2,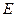 为
为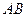 的中点,设直线
的中点,设直线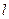 过点
过点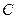 且垂直于矩形
且垂直于矩形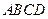 所在平面,点
所在平面,点 是直线
是直线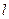 上的一个动点,且与点
上的一个动点,且与点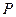 位于平面
位于平面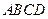 的同侧。
的同侧。
(1)求证: 平面
平面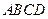 ;
;
(2)设二面角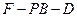 的平面角为
的平面角为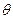 ,若
,若 ,求线段
,求线段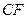 长的取值范围。
长的取值范围。
推荐套卷
如图1,在平面内,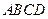 是
是 的矩形,
的矩形,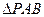 是正三角形,将
是正三角形,将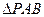 沿
沿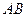 折起,使
折起,使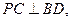 如图2,
如图2,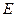 为
为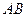 的中点,设直线
的中点,设直线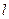 过点
过点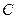 且垂直于矩形
且垂直于矩形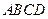 所在平面,点
所在平面,点 是直线
是直线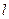 上的一个动点,且与点
上的一个动点,且与点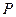 位于平面
位于平面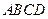 的同侧。
的同侧。
(1)求证: 平面
平面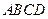 ;
;
(2)设二面角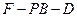 的平面角为
的平面角为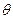 ,若
,若 ,求线段
,求线段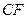 长的取值范围。
长的取值范围。